In this post we discuss retractions and deformation retractions in algebraic topology. Positive as well as negative examples are presented to illustrate the two concepts.
I. Retractions
Definition (Homotopy) Two continuous maps \(f,g:X\to Y\) are said to be homotopic if there is a continuous map \(H:X\times[0,1]\to Y\) such that \(H(x,0)=f(x)\) and \(H(x,1)=g(x)\) for all \(x\in X\). In this case \(H\) is called a homotopy between \(f\) and \(g\), and we write \(f\simeq g\).
Definition (Retraction) Let \(X\) be a topological space and let \(A\) be a subspace of \(X\). Then the map \(r:X\to A\) is called a retraction if it is continuous, and \(r(a)=a\) for all \(a\in A\) (i.e. \(A\) is kept fixed).
Note that the range of the retraction map is the subspace \(A\), not \(X\).
Example 1.1 Let \(X\) be any nonempty topological space and let \(x_0\in X\) be an arbitrary point. Then \(r:X\to\{x_0\}\) defined by sending all points of \(X\) to \(\{x_0\}\) is trivially a retraction.
Example 1.2 Another trivial case: the identity map \(\mathbb{I}:X\to X\) is a retraction.
Example 1.3 A common example is to map the unit disk \(D^2\) to a smaller closed concentric disk \(\bar{D}(0,\varepsilon)\) of radius \(\varepsilon<1\). Every \(v\in D^2, v\notin \bar{D}(0,\varepsilon)\) is mapped to \((\varepsilon/\|v\|)v\) on the boundary, while points of \(\bar{D}(0,\varepsilon)\) are kept fixed.
In all examples above, the subspace \(A\) always seems to be closed. In fact, this is typical:
Proposition If \(r:X\to A\) is a retraction, and \(X\) is Hausdorff, then \(A\) is closed in \(X\).
Proof 1. We prove \(X\setminus A\) is open. Let \(x\in X\setminus A\). Then \(r(x)\in A\) so that \(x\neq r(x)\). Since \(X\) is Hausdorff, we can find two open neighborhoods \(U\) and \(V\) of \(x\) and \(r(x)\) respectively, such that \(U\cap V=\varnothing.\) Then \(r^{-1}(V)\) is open, since \(r\) is continuous, and further more \(x\in r^{-1}(V)\), so that \(r^{-1}(V)\cap U\) is an open neighborhood of \(x\). We claim that \(r^{-1}(V)\cap U\) is disjoint from \(A\), from which the closeness of \(A\) follows. Let \(y\in r^{-1}(V)\cap U\). Then \(y\in U\), while at the same time \(r(y)\in V\). Since \(U\cap V=\varnothing\), \(y\neq r(y)\), so that \(y\notin A\). This completes the proof.
Proof 2. Define a continuous function \(F\) from \(X\) to \(X\times X\) by sending each \(x\in X\) to \((x,r(x))\). Let \(D=\{(x,x)\,\vert\, x\in X\}\) denote the diagonal of \(X\times X\), which is closed in \(X\times X\). Then \(F^{-1}(D)=\{x\in X\,\vert\, x=r(x)\}=A\) is closed.
A retraction may be “too abrupt”, like example 1.1, even if the map itself is technically continuous. If \(r\) can continuously shrink space \(X\) to subspace \(A\) (or “slowly”, “smoothly”, “gently” in a loose sense), then we say that \(r\) is a deformation retraction.
II. Deformation Retractions
Notation For \(A\subset X\), we use \(\iota:A\to X\) to denote the inclusion map. (i.e., \(\iota(a)=a\) for all \(a\in A\))
Definition (Deformation Retraction) Let \(X\) be a topological space and let \(A\) be a subspace of \(X\). Let \(r:X\to A\) be a retraction. \(r\) is called a deformation retraction if the identity map \(\mathbb{I}:X\to X\) and \(\iota\circ r:X\to X\) are homotopic, namely there exists a homotopy \(H:X\times[0,1]\to X\) such that \(H(x,0)=x\) and \(H(x,1)=(\iota\circ r)(x)=r(x)\) for all \(x\in X\).
Note 1. The inclusion map \(\iota\) here is just a convenient tool for placing \(A\) in \(X\), to make \(\mathbb{I}\) and \(r\) “comparable” (have the same range), so that we can talk about homotopy between them.
Note 2. The composite map \(\iota\circ r\) is continuous from \(X\) to \(X\). For example, let \(r:X\to\{x_0\}\) be a retraction to a point, so that \(\iota\circ r\) is a constant map from \(X\) to \(X\). Then given an arbitrary open set \(V\) in \(X\), there are only two possibilities: either \(V\) does not contain \(x_0\), in which case \((\iota\circ r)^{-1}(V)=\varnothing\), or \(x\) is in \(V\), so that \((\iota\circ r)^{-1}(V)=X\). In either case, the inverse image is (trivially) open.
One should distinguish between retraction and deformation retraction. The former only requires \(r\) itself to be continuous, which can be trivially achieved as in Example 1.1. The later requires \(H\) to be continuous, thus the notion of “continuously shrinkage”. Deformation retraction has stronger requirement on the space \(X\).
Example 2.1 Let \(U\) and \(V\) be two disjoint open disks in \(\mathbb{R}^2\) and let \(X=U\cup V\). We can imagine \(X\) to be two plates separately placed on on a table. Pick a point \(x_0\) in \(V.\) Then the map \(r:U\cup V\to\{x_0\}\) that sends all points of \(X\) to \(\{x_0\}\) is a retraction. However, it cannot be a deformation retraction. If you just keep shrinking the two disks without moving one into the other, then the resulting space will be two points. You could also map all points of \(U\) into \(V\) at some time, and then shrink \(V\) afterwards, but this construction cannot be continuous. Let’s say at some time \(t_0\in[0,1]\), \(U\) is mapped into an open neighborhood \(W\subset V\) of \(x_0\). Then \(H^{-1}(W)=U\times[t_0,1]\cup V\), which is not open. The problem is that this sudden change causes discontinuity in \([0,1]\), contrary to the notion of “continuously deforming the space”.
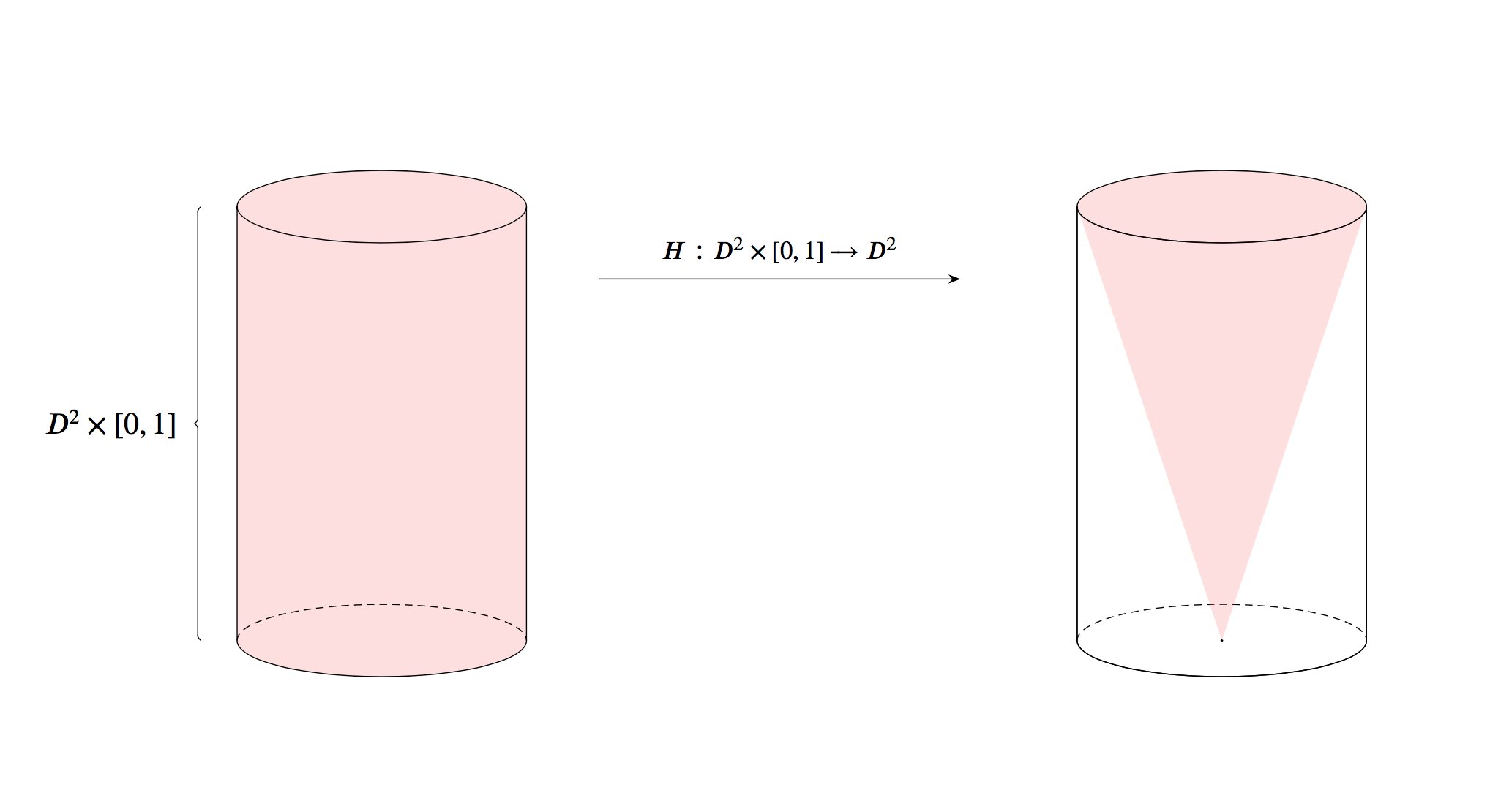
Example 2.2 The following picture shows that the unit disk \(D^2\) in \(\mathbb{R}^2\) can be continuously shrunk to the origin.

You might want to carefully distinguish between the homotopy \(H\) and the map \(r\). The homotopy \(H\) is a collection of functions from \(D^2\) to a subspace of \(D^2\), including all functions shown above, each with a different range. In particular, \(H\) includes the identity \(\mathbb{I}\) as well as \(r\). The homotopy \(H\) organizes them together “in a continuous way”. \(r:D^2\to\{0\}\) is a always a retraction. But deformation retraction requires that such an \(H\) exists so that we can start from the identity and continuously evolve to \(r\).
Example 2.3 The following picture shows that \(D^2\setminus\{0\}\) can be continuously retracted to the unit circle \(S^1\).
This is pretty intuitive, but why we are not able to do the same thing for \(D^2\)?
From algebraic topology we know that \(D^2\) and \(S^1\) have different fundamental groups: for \(S^1\) it is \(\mathbb{Z}\), while for \(D^2\) it is trivial (namely \(\{0\}\)). But here let’s look at an elementary argument: the map \(r:D^2\to S^1\) defined by mapping each ray emanated from the origin to its intersection with \(S^1\), and by mapping the origin to any point \(z\in S^1\) cannot be continuous. For a neighborhood \(V\) of \(z\) such that \(V\neq S^1\), the inverse image of \(V\) is the union of an open set in \(D^2\) with the (closed) point \(\{0\}\), thus it cannot be open. Of course, there may be other possibilities, and this is why fundamental groups are useful. But one can see that the origin \(\{0\}\) is “too annoying”, and place it in anywhere will cause discontinuity.
Example 2.4 It is important to note that, in the process of shrinking a space \(X\), we must always stay whinin the space \(X\) and not go outside of it. So, for example, the following “shrinkage” is not a deformation retraction:

Here the space \(X\) is a segment of the torus \(S^1\times S^1\). As one tries to shrink it, the resulting spaces are no longer part of \(X\), so by our definition such a mapping is not deformation retraction.
From the algebra side, the torus segment has \(\mathbb{Z}\times\{0\}\) as its fundamental group, while for a line segment it is trivial, so there cannot be a deformation retraction. Likewise, a full torus \(S^1\times S^1\) has fundamental group \(\mathbb{Z}\times\mathbb{Z}\), so it cannot continuously shrink to a circle, whose fundamental group is $\mathbb{Z}$.
By the way, If we replace \(S^1\times S^1\) by \(D^2\times S^1\), i.e., the solid torus, then such shrinkage like the figure above is a deformation retraction.
In 2D, we might think of shrinking a circle to its center. The center is not part of the circle, so such shrinkage is also not a deformation retraction. From the algebra side, \(S^1\) has fundamental group \(\mathbb{Z}\), while a point has the trivial fundamental group, so no such deformation retraction would exist.
III. Homotopy Equivalence
From the above discussion we find that, for a deformation retraction \(r:X\to A\), we have \(\iota\circ r\simeq\mathbb{I}\) and \(r\circ\iota\simeq\mathbb{I}_{A}\) (in fact \(r\circ\iota=\mathbb{I}_{A}\)). Since in this case, \(X\) can be “continuously deformed” into \(A\), the two spaces are in some sense “equivalent”. We call this equivalence “homotopy equivalence”:
Definition (Homotopy Equivalence) Two topological spaces \(X\) and \(Y\) are called homotopy equivalent if there exist a continuous map \(f:X\to Y\) and a continuous map \(g:Y\to X\) such that \(g\circ f\simeq\mathbb{I}_{X}\) and \(f\circ g\simeq\mathbb{I}_{Y}\). The map \(f\) is called a homotopy equivalence.
Summary
In this post, I presented definitions of retractions and deformation retractions in algebraic topology, and illustrated their differences by several examples. We can generalize deformation retraction to the concept of homotopy equivalence.
Cite as:
1
2
3
4
5
6
7
@article{lifei2022retraction,
title = "Deformation Retractions are 「Continuous」 Retractions",
author = "Li, Fei",
journal = "https://lifeitech.github.io",
year = "2022",
url = "https://lifeitech.github.io/posts/deformation-retraction/"
}
Comments powered by Disqus.