We provide a picture for visualizing the concept of double dual in linear algebra and functional analysis. We show that, every vector in a vector space $V$ naturally corresponds to a function that maps functionals on $V$ to numbers, namely evaluation of functionals on that vector. Conversely, thanks to a finite basis, every element in the double dual can be represented as such evaluation function for finite dimensional vector spaces.
Definition (Linear Functional) Let $V$ be a finite dimensional real vector space. A linear functional on $V$ is a linear map from $V$ to $\mathbb{R}$. Namely, $f:V\to\mathbb{R}$ is a linear functional if
- $f(v_1 + v_2) = f(v_1) + f(v_2)$ for all $v_1,v_2\in V$;
- $f(\alpha v) = \alpha\cdot f(v)$ for all $\alpha\in\mathbb{R}$ and $v\in V$.
Definition (Dual Space) Let $V$ be a finite dimensional real vector space. Its dual space, denoted by $V^*$, is the set of all linear functionals on $V$.
\[V^* = \big\{f:V\to\mathbb{R}\mid f \text{ is linear}\big\}\]The dual space is also a vector space: if \(f,g\in V^*\), then \(f+g\in V^*\) and \(\alpha f\in V^*\) for any \(\alpha\in\mathbb{R}\). Furthermore, given a basis $(v_1,\ldots, v_n)$ of $V$, it is possible to construct the dual basis $(f_1,\ldots,f_n)$ in $V^*$ where for any $v=\alpha_1v_1+\cdots+\alpha_nv_n\in V$,
\[f_1(v)=\alpha_1,\,\ldots,\,f_n(v)=\alpha_n.\]This implies that $V$ and its dual space $V^*$ are isomorphic.
Definition (Double Dual) The dual space of \(V^*\), denoted by \(V^{**}\), is called the double dual. Namely, the double dual is the set of all linear functionals on \(V^*\).
\[V^{**} = \big\{\varphi:V^*\to\mathbb{R}\mid \varphi \text{ is linear}\big\}\]As before, the double dual is a vector space. If $\varphi_1$ and $\varphi_2$ are linear mappings defined on $V^*$, then for $a,b\in\mathbb{R}$, the mapping $a\,\varphi_1+b\,\varphi_2$ is again linear, so \(a\,\varphi_1+b\,\varphi_2\in V^{**}\). Since $V$ and its dual \(V^*\) are isomorphic, it follows immediately that \(V^*\) and \(V^{**}\) are isomorphic, and consequently $V$ and its double dual \(V^{**}\) are isomorphic.
The connection between $V$ and \(V^{**}\) can be seen in a more direct way. For each $v\in V$, there is a \(\varphi_v\in V^{**}\) defined by
\[\begin{align} \varphi_v: V^*&\to\mathbb{R},\\[1em] f&\mapsto f(v)\in\mathbb{R},\quad f\in V^* \end{align}\]The function $\varphi_v$ maps any functional $f\in V^*$ to a real value, while $f$ maps any vector $v\in V$ to a real value. This isomorphism $v\mapsto\varphi_v$ is canonical. The picture below provides a visualization of this canonical isomorphism.
 Double Dual Visualization. $V$ and $V^{**}$ are isomorphic. For every $v\in V$ there corresponds a \(\varphi_v\in V^{**}\) that maps any $f\in V^*$ to $f(v)\in\mathbb{R}$.
Double Dual Visualization. $V$ and $V^{**}$ are isomorphic. For every $v\in V$ there corresponds a \(\varphi_v\in V^{**}\) that maps any $f\in V^*$ to $f(v)\in\mathbb{R}$.
Each element in $V$ is like a “magnet” that can “attract” linear functionals in \(V^*\). Imagine we grab some linear functionals \(\{f_1,f_2,\ldots\}\) from the bag \(V^*\), and throw them toward a vector $v\in V$. After they hit $v$, they are converted to their “values” at $v$.
\(v_1\) and \(v_2\) in the figure are like “touchstones” that “test” values for any \(f\in V^*\). Since \(f: V\to\mathbb{R}\) can have different values at different vectors in \(V\), when we throw the same set of \(f\)s to a different vector, say \(v_3\in V\), the resulting values would be different. Each \(v\in V\) acts like a mapping from the domain \(V^*\) to real numbers. In this sense, we can identify each vector in \(V\) with an element in its double dual \(V^{**}\).
On the other hand, given any \(\varphi\in V^{**}\), it is also possible to find a $v\in V$ such that
\[\varphi(f)=f(v)\]for any \(f\in V^*\).
Let $(v_1,\ldots,v_n)$ be a basis in $V$, and let $(f_1,\ldots,f_n)$ be the dual basis in $V^*$, and finally let $(\varphi_1,\ldots,\varphi_n)$ be the dual basis in \(V^{**}\). For
\[\varphi=\alpha_1\,\varphi_1+\cdots+\alpha_n\,\varphi_n\]we prove that
\[v=\alpha_1\,v_1+\cdots+\alpha_n\,v_n\in V\]is the desired vector. We can represent any \(f\in V^*\) as $f=\beta_1f_1 + \cdots + \beta_n f_n$ for some scalars $\beta_1,\ldots,\beta_n\in\mathbb{R}$. Then,
\[\begin{split} \varphi(f) &= \alpha_1\varphi_1(f) + \cdots + \alpha_n\varphi_n(f)\\[1em] &= \alpha_1\varphi_1(\beta_1f_1 + \cdots + \beta_n f_n) + \cdots + \alpha_n\varphi_n(\beta_1f_1 + \cdots + \beta_n f_n)\\[1em] &= \alpha_1\beta_1 + \cdots + \alpha_n\beta_n. \end{split}\]On the right hand side, we have
\[\begin{split} f(v) &= \beta_1f_1(v) + \cdots + \beta_nf_n(v)\\[1em] &= \beta_1f_1(\alpha_1\,v_1+\cdots+\alpha_n\,v_n) + \cdots + \beta_nf_n(\alpha_1\,v_1+\cdots+\alpha_n\,v_n)\\[1em] &= \beta_1\alpha_1 + \cdots + \beta_n\alpha_n. \end{split}\]We find that $\varphi(f)=f(v)$ for any \(f\in V^*\). The proof is now complete.
Finally, we mention that, the finite dimensional case that we have discussed above does not generalize to infinite dimensions. If $V$ is an infinite dimensional vector space, then its (algebraic) dual space always has a larger dimension than $V$. The double dual is thus also strictly larger than $V$.
Cite as:
1
2
3
4
5
6
7
@article{lifei2022dual,
title = "Visualizing the Double Dual",
author = "Li, Fei",
journal = "https://lifeitech.github.io",
year = "2022",
url = "https://lifeitech.github.io/posts/double-dual/"
}
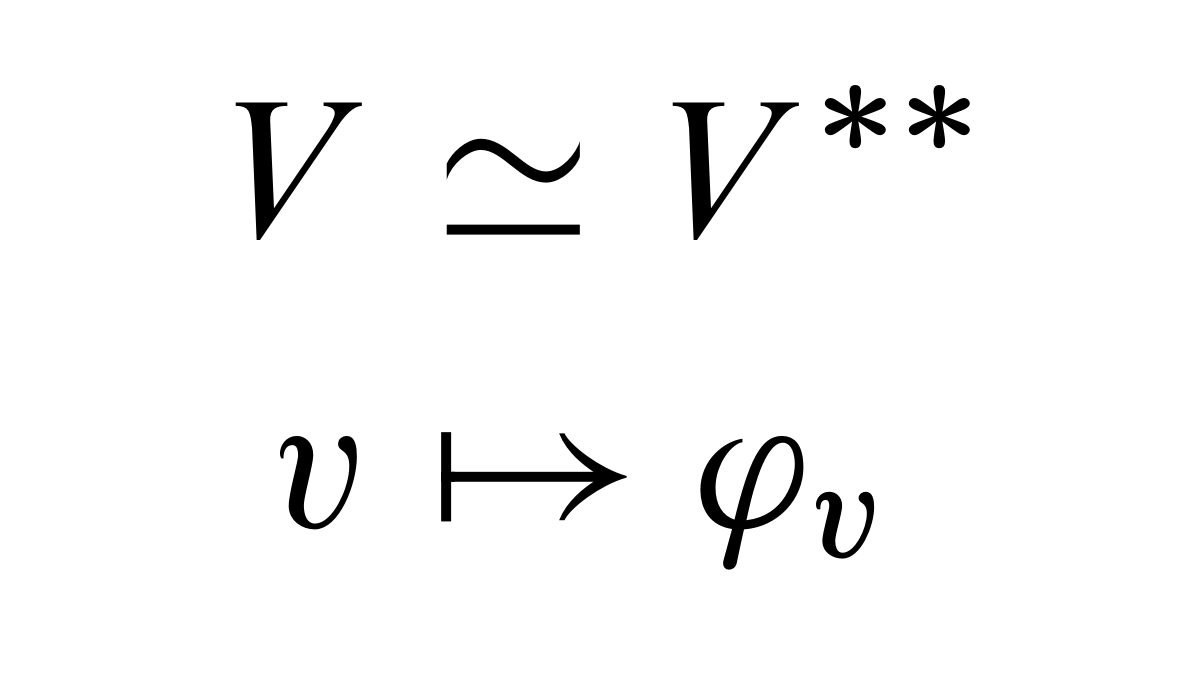
Comments powered by Disqus.