Here you can find some of my course notes taken during my past studies. Subjects include machine learning, algorithms, probability, statistics, stochastic process, optimal control, general topology and more.
- Notes on Machine Learning
- Course Notes for Statistics and Probability
- Course Notes for Algorithms
- Course Notes for Optimization
- Course Notes for Stochastic Process
- Course Notes for Microeconometrics
- Course Notes for Time Series
- Notes for General Topology
- Bilinear Forms and Sesquilinear Forms
- An Introduction to Set Theory
Notes on Machine Learning
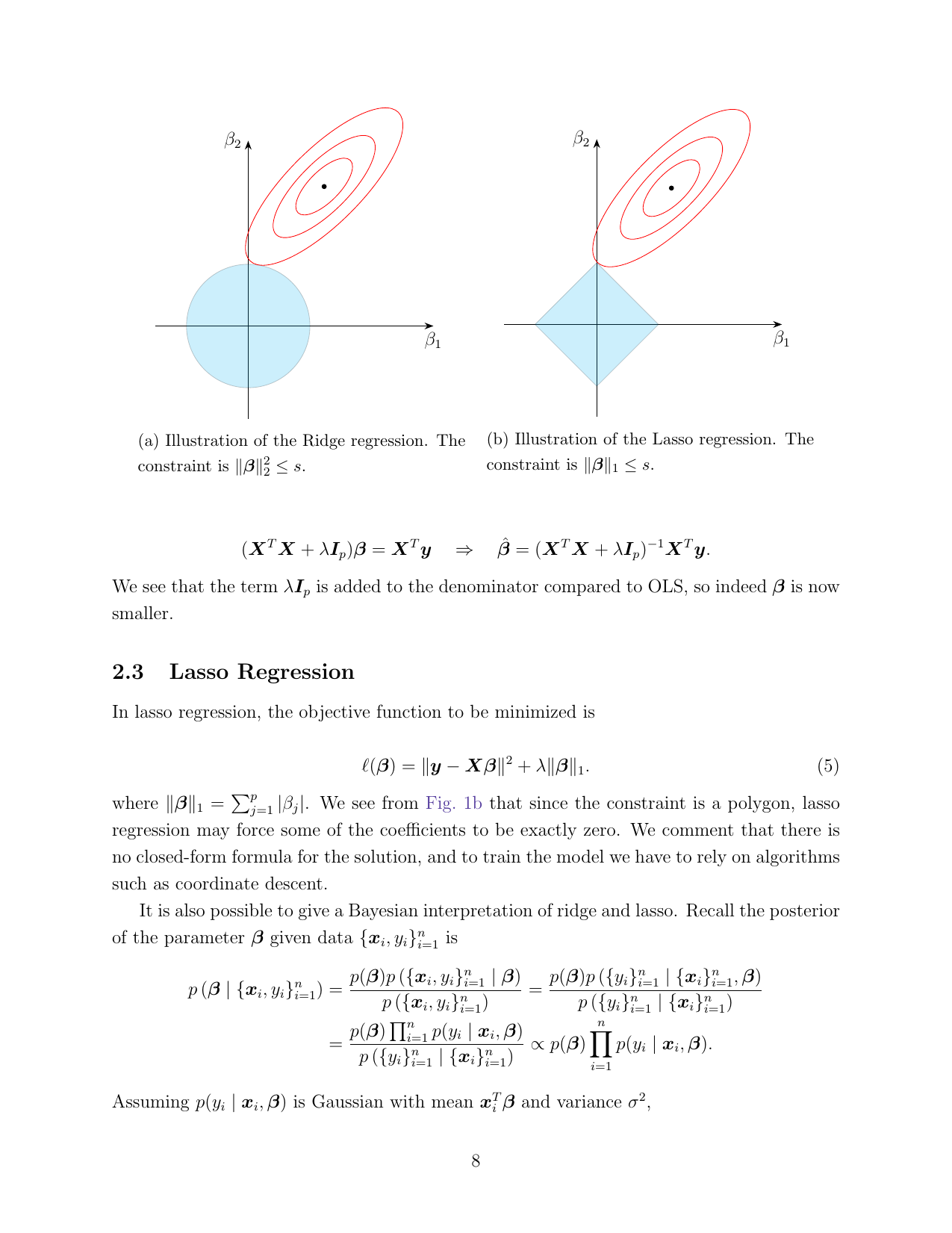
Common models in machine learning are discussed, including linear regression, logistic regression, Gaussian discriminant analysis, naive Bayes, splines, decision trees, gradient boosting and support vector machines. This notes focus on the mathematical derivation of those models. Highlights:
- a derivation of online linear regression formula;
- logistic regression parameter estimation;
- derivation of the AdaBoost as a gradient boosting algorithm with exponential loss function;
- a proof that AUC is the probability that a classifier ranks a randomly chosen positive sample higher than a randomly chosen negative sample.
Course Notes for Statistics and Probability
First there is a quick rundown of the basics of probability theory, then a significant portion is devoted to parametric inference. Topics include sufficient statistics, Fisher information, ancillarity and completeness, maximum likelihood estimation, Cramér-Rao bound, hypothesis testing. In addition, bootstrap, the EM algorithm, simulations and principal component analysis (PCA) are also explained in detail.
Course Notes for Algorithms
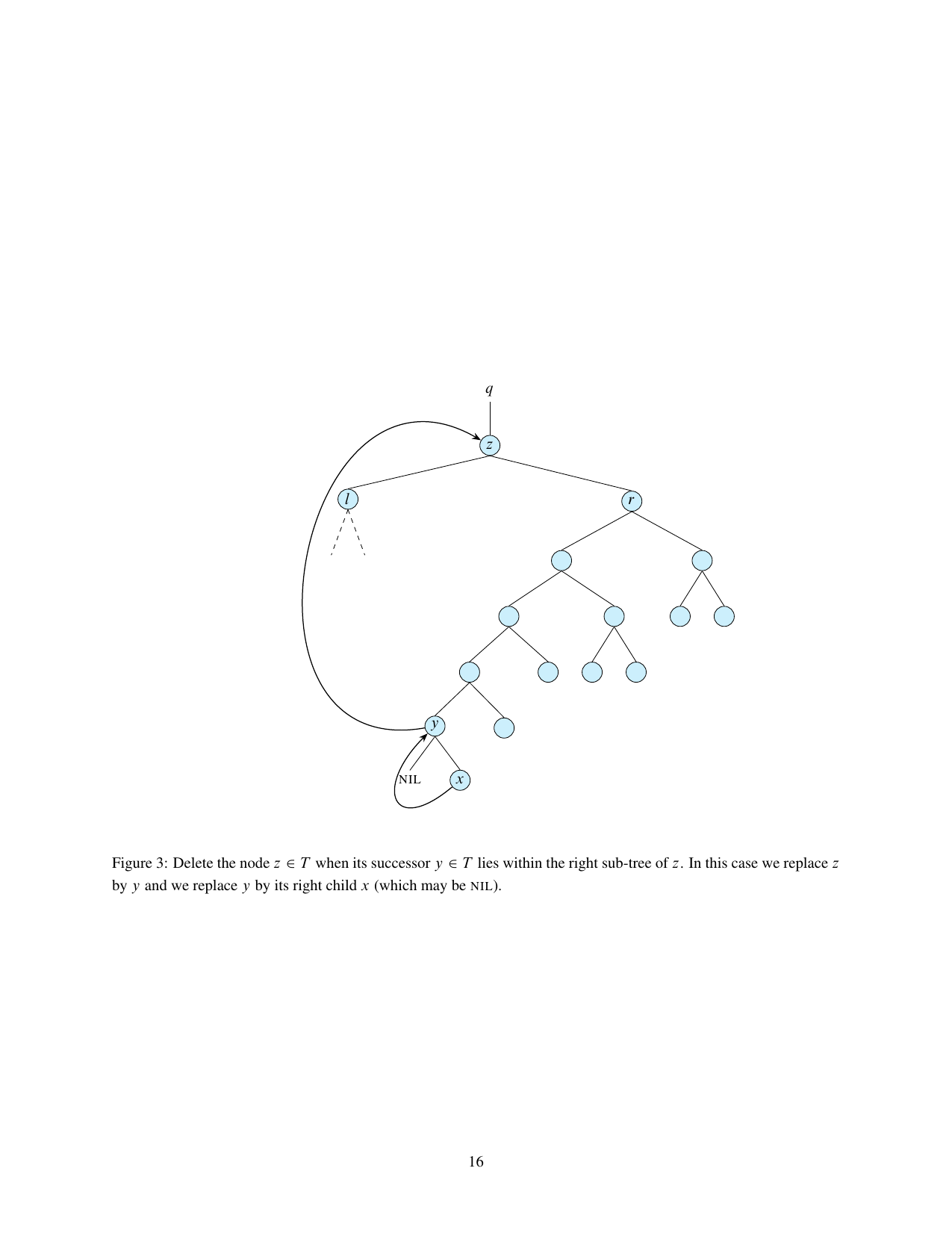
Course notes for algorithms course. Part of the course followed Cormen’s Introduction to Algorithms . Besides data structures (stacks, linked lists, BSTs, hash tables etc.) and sorting algorithms, the notes contain a detailed documentation for graph algorithms, including the Prim’s algorithm, the Bellman-Ford Algorithm, Dijkstra’s algorithm, the Floyd-Warshall algorithm and so on, as well as several dynamic programming problems. Randomized algorithms are also discussed, including the Karger’s min-cut algorithm.
Course Notes for Optimization
This is my course notes on optimal control theory. First we discuss Banach spaces and Hilbert spaces. Full proofs are given to the Banach fixed point theorem, the Schauder’s fixed point theorem and the Riesz representation theorem. Next, in section 3, we discuss calculus of variations, including the famous Euler-Lagrange equation. Section 4 includes an introduction to optimal control problems and the Bang-bang principle. Finally the Pontraygin maximum principle and dynamic programming are discussed. Many examples are present in the notes.
Course Notes for Stochastic Process
The course followed Erhan Çinlar’s book Probability and Stochastics. Topics include measure and integration, probability theory, martingales, Poisson random measures, Lévy processes and Brownian motion.
Course Notes for Microeconometrics
Topics include causality, linear regression, t test and F test, difference in difference (DID), instrumental variables (IV) and regression discontinuity design (RDD).
Course Notes for Time Series
The first part of the note is univariate time series analysis. Topics include stationary process, autocovariance function, ARMA models, invertibility, model estimation and forecasting. The second part is multivariate time series analysis. Topics include estimation, forecasting and interpretation of VARMA models.
Notes for General Topology
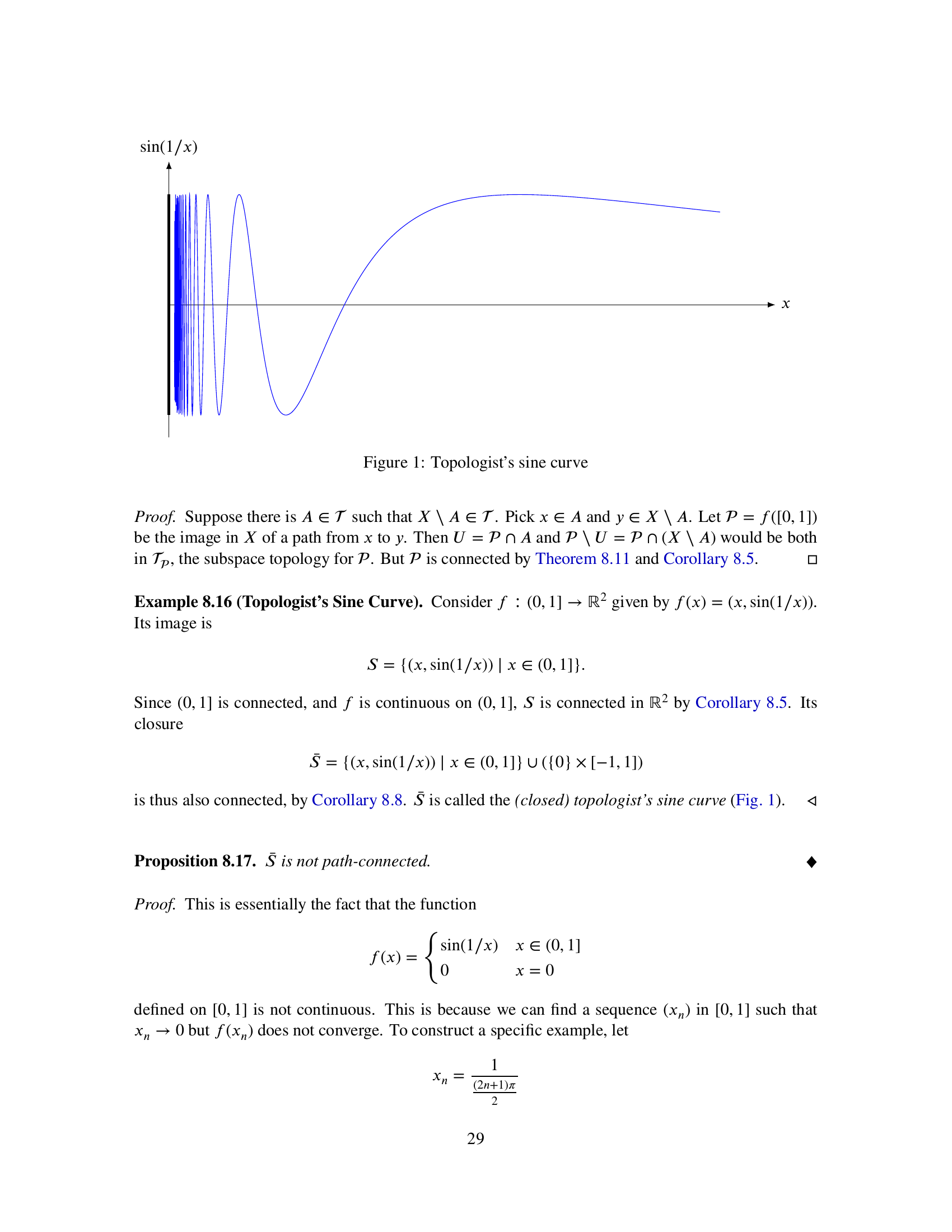
This is the course note that I gave to students when I was a teaching assistant for the Mathematical Economics course at Shandong University, where part of the course covered general topology. We start from metric spaces, and then cover all essential concepts in general topology, including basis, convergence, continuity, connectedness, and compactness. We also discuss some advanced topics such as countability, separation properties and Urysohn lemma.
Bilinear Forms and Sesquilinear Forms
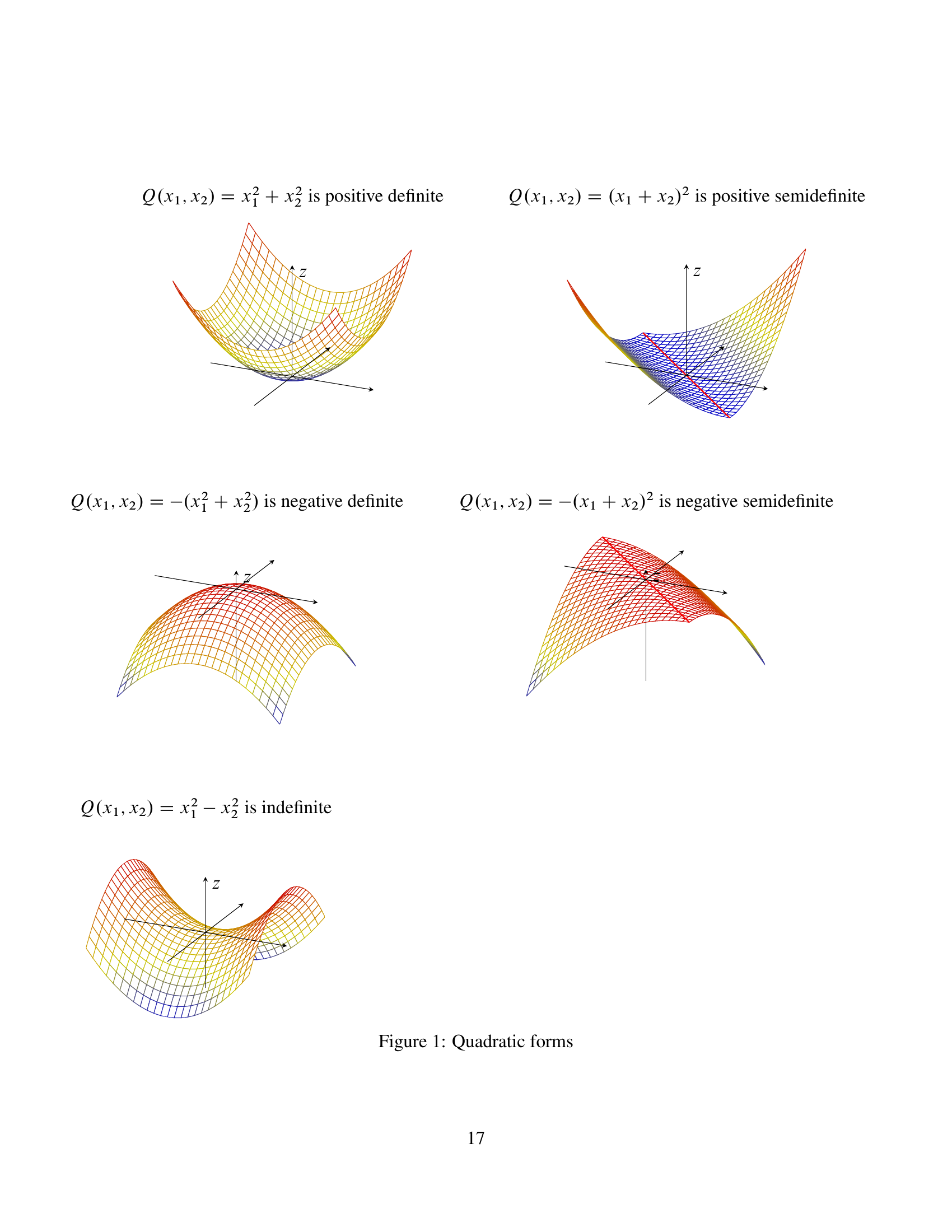
In this article, we give a detailed look at bilinear and sesquilinear forms in linear algebra. We’re interested in conditions under which a form possesses an orthonormal basis. It turns out that this is true if and only if it is (Hermitian) symmetric and positive definite. We show that the symmetry condition is due to symmetry of orthogonality. We then discuss operators and quadratic forms using our theory of bilinear forms.
An Introduction to Set Theory
In this article, we give a quick introduction to set theory. Section 1 contains a review of algebra of sets, functions, and power sets. Section 2 discusses Russell’s paradox, following which we mention the axiom of specification in ZFC set theory. Sections 3 is on countability and uncountability of sets. We prove basic properties of countable sets, and then give a discussion of the Continuum Hypothesis.